CS143 Lecture04 Implementation of Lexical Analysis

Implementation of regular expressions:

$$RegExp ⇒ NFA ⇒ DFA ⇒ Tables$$

Notation

• Union: $$A|B\equiv A+B$$
• Option: $$A+\epsilon\equiv A? $$
• Range: $$‘a’+‘b’+…‘z’\equiv [a-z]$$
• Excluded range: $$complement\ of\ [a-z]\equiv [\hat{} a ]$$

Regular Expressions => Lexical Spec. (1)

1. Write a regex for each token

2. Construct R, matching all lexemes for all tokens
   $$
   R = Keyword + Identifier + Number + …\
   = R1+ R2+ …
   $$
   (This step is done automatically by tools like Flex)

3. Let input be $$x_1…x_n$$ (iterate chars in input)

   For $$i \le i \le n$$ check
   $$
   x_1…x_i \in L®
   $$

4. If success, then we know that

   $$x_1…x_i \in L(R_j)$$ for some $$j$$

5. Remove $$x_1…x_i$$ from input and goto (3)

Ambiguities (1)

当
$$
x_1…x_i\in L®\
x_i…x_k\in L®
$$
上述两式同时成立时，换句话说，也就是多个起点相同，长度不同的子串同时满足语言$$L®$$时，

**Rule: ** Pick longest possible string in $$L®$$

也就是说取满足$$L®$$的最长子串。

Ambiguities (2)

当相同子串满足多个正则语言定义时，即
$$
x_1…X_i\in L(R_j)\
x_i…x_i\in L(R_k)
$$
这种给个优先级就好惹。

Error Handling

考虑如果一段输入的前缀无法被任何规则匹配的情况，我们会一直匹配直到输入终结处（EOF）。我们可以尝试编写一个匹配所有坏字符串的规则，并将其优先级设为最低。

Summary

Regular expressions provide a concise notation for string patterns.

Use in lexical analysis requires small extensions

• To resolve ambiguities
• To handle errors

Good algorithms known

• Require only single pass over the input
• Few operations per character (table lookup)

Finite Automata

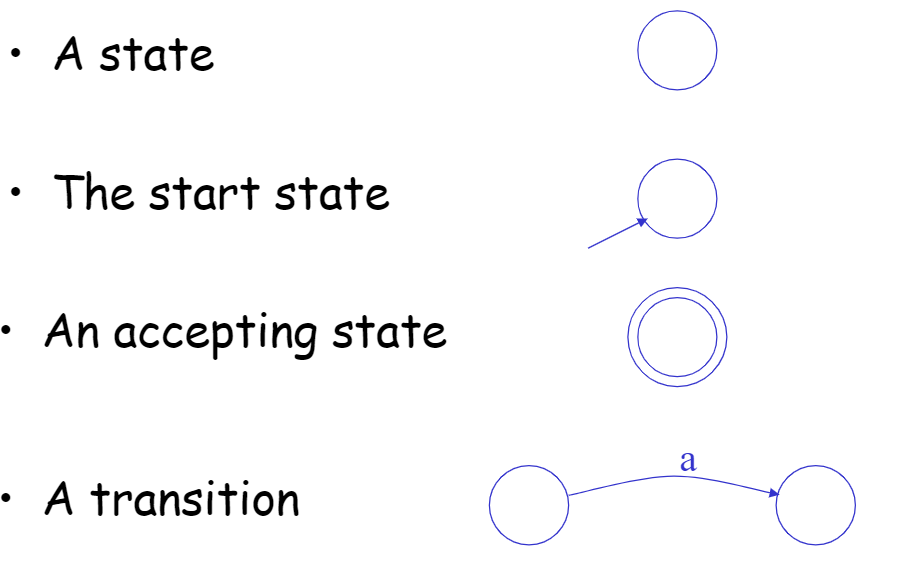
A finite automaton consists of

• An input alphabet $$\sum$$
• A set of states $$S$$
• A start state $$n$$
• A set of accepting states $$F \subseteq S$$
• A set of transitions $$state \rightarrow^{input} state$$

Transitions

中文也就是状态转换。可以记作
$$
s_1 \rightarrow^{a} s_2
$$
可以读作输入$$a$$使状态$$s_1$$转移到状态$$s_2$$。

如果在输入结束时不处于接受状态(accept)，则拒绝(reject)该输入。

Epsilon Moves

This is a way to change a state to another without any input. 不过我真没找到这玩意的中文翻译，所以以下叫做ε-moves（大草

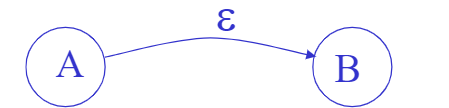
Only exist in NFAs.

Deterministic and Nondeterministic Automata

• Deterministic Finite Automaton

  每个输入都有确定的一个状态转移。

  没有ε-moves。

• Nondeterministic Finite Automata

  对于每个输入，状态转移的个数不确定。可以是零、一或多个状态转移。

  可以含有ε-moves。

所以，对于DFA来说，整个状态转移路径可以使用一个给定的输入确定。NFA则可以选择多种状态转移路径或是进行ε-moves。

因此我们规定：一个$$NFA$$如果可以达到一个最终状态，那么它是接受的（accept）。

$$NFA$$ vs. $$DFA$$

• $$DFA$$通常比$$NFA$$快
• $$DFA$$通常比$$NFA$$复杂（甚至可以达到指数级的）

对于$$NFA$$，它的状态数是可能状态数$$N$$的非空子集。也就是说，有$$2^N-1$$个可能状态数。

Convert Regular Expression to Finite Automata

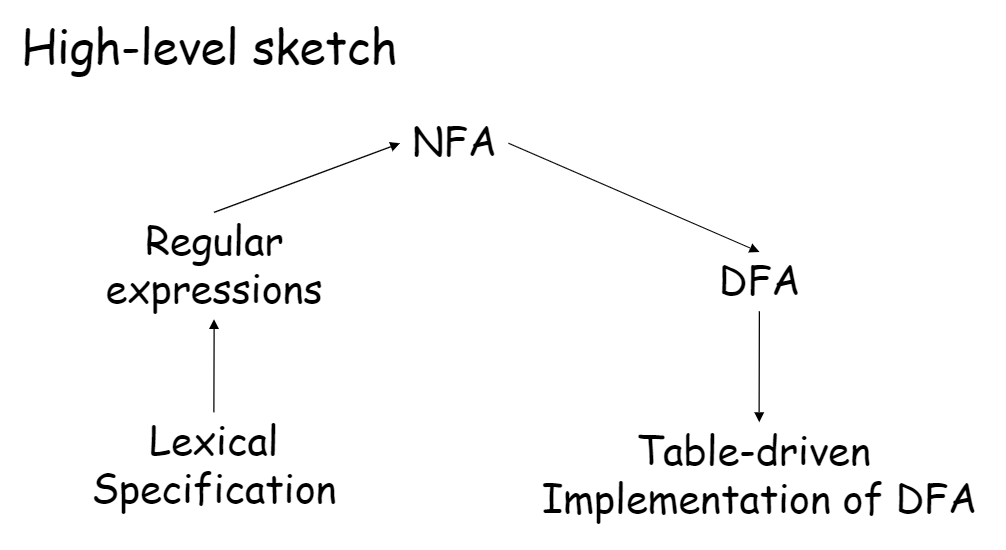
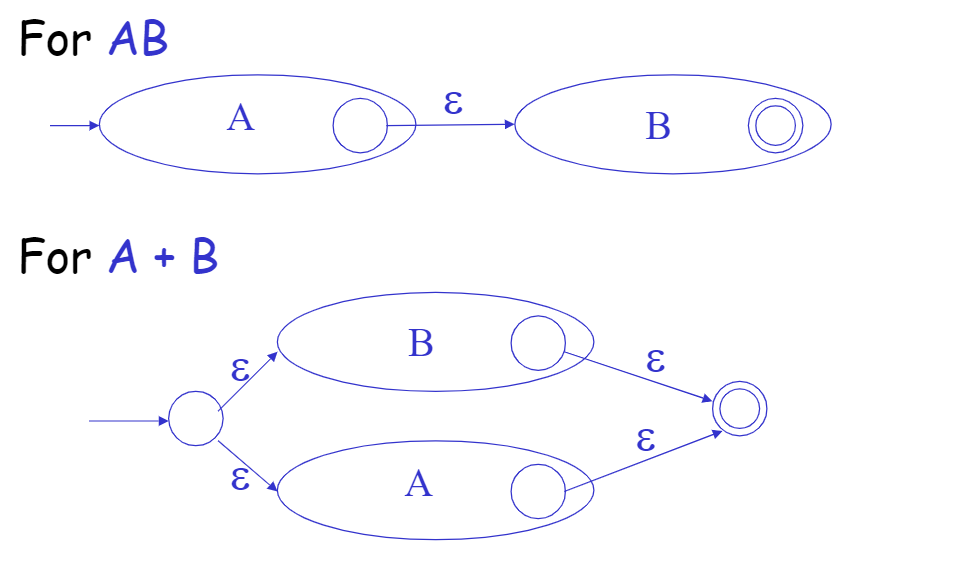
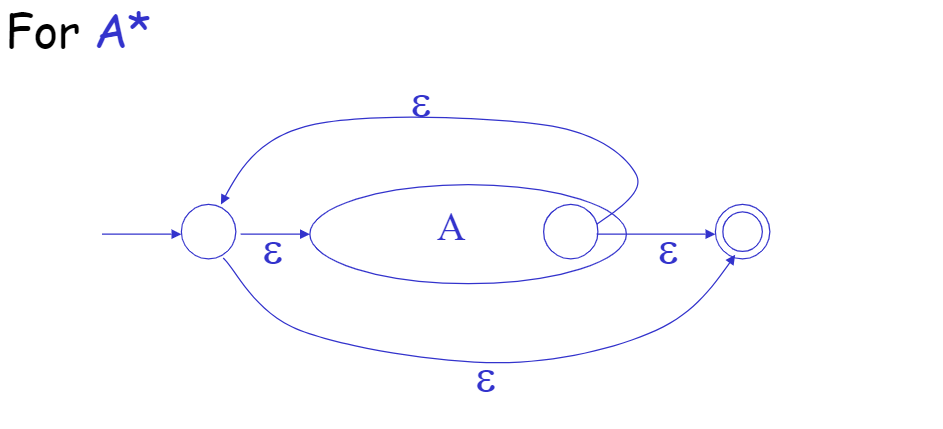
技巧

我们可以对$$NFA$$进行模拟。且目标$$DFA$$的每个状态都是一个$$NFA$$状态的非空子集。

目标$$DFA$$起始状态是一组从$$NFA$$的起始状态可以通过ε-moves转移到的状态。

而对于其它转换规则，我们遵从——如果状态$$S^$$在遇到输入$$a$$时，可以从原状态$$S$$达到（包括*ε-moves*），那么我们将$$S \rightarrow^{a} S^$$放进$$DFA$$的转换规则列表中。

实现

$$DFA$$可以通过一个二维数组$$T$$实现，我们将$$S_i\rightarrow^{a}S_k$$映射为$$T[i,a]=k$$。所以，$$T$$的一个维度代表状态，而另一个维度代表输入，其值代表目标状态。

执行$$DFA$$

如果当前状态为$$S_k$$，在读取输入$$a$$后，查表转移到状态$$S_i=T[k,a]$$。

结论

将$$NFA$$转换到$$DFA$$是很多像$$Flex$$这种工具的核心。但是因为$$DFA$$可能会有着极其巨大的状态数，所以，实践中通常会牺牲时间来换取空间。