『闲谈』 形式语言与正则语言

Formal Languages vs. Regular Languages

Formal Languages 中文叫做形式语言，而 Regular Languages 叫做正则语言。而这两个概念单靠其中文名来理解，是容易让人迷惑的，也就是不能顾名思义了。

首先，这两者都需要给出一个字母表（英文：alphabet）$\sum$，也就是包含所有可能出现的字符的集合。字母表是由非空符号或字型组成的有限集合，也就是语言中出现的符号、字母（英文：letter，也就是单个字¹）以及其它词元的集合。照习惯称这个集合为字母表，但是可能叫做字符表或是词汇表会更好一些。注意字母表是一个有限集合（英文：finite set）。

在这里再给出一些记号（notation）以及定义（definition）。

字母表所构成的所有单词（words）的集合记作$\sum^{*}$，可以读作字母表的闭包（名字怪怪的不是嘛，见下文）。将语言$A$记作$L(A)$，读作语言$$A$$。我们将空字符串记作$\epsilon = {“”}$²，读作epsilon，在非确定有限自动机（NFA）中起到了重要作用。

单词（word）是字母表中元素组成的的有限序列（要注意这里称之为序列而不是集合）。比如语言$X={0,1}$中，$0$、$011$、$1111$等称为语言$X$的中单词。

而上面提到的闭包（英文：Kleene closure，克林闭包）笼统的定义就是由零个、一个或多个（就是任意个）字母表中的元素互相连接所组成的集合，记作$A^=\cup_{i\ge 0}A^i$。这里的闭包应与计算机科学（英文：computer science）*中的捕获自由变量的函数区分开来，两者没有什么联系。这里之所以叫做闭包，是因为在这个集合（也就是闭包运算所产生的字符串集合）上定义的运算（并、闭包运算，并运算也被称为连接运算）的运算结果也在这个集合中，也就说满足了封闭性（是不是想起了群公理）。这里给出语言$$A$$的闭包的更简单的定义：

$$A^*=\epsilon|A|AA|AAA|…$$

现在回归正题。

基于字母表$\sum$，所谓形式语言，就是由该字母表上单词（word）组成的集合。也有一个等价的定义——字母表$\sum$上的形式语言是字母表闭包$\sum^{*}$的一个子集（英文：subset）。

而正则语言（regular language/rational language，也称为正规语言），是一种可以被正则表达式（英文：regular expression）所定义的形式语言，所以正则语言相当于形式语言的一类子集。

顺便，上面的提到的正则表达式由$\epsilon$、$\sigma\in \sum$、$(r_1)^*$、$(r_1+r_2)$、$(r_1 r_2)$（当且仅当$r_1$、$r_2$为正则表达式）组成。其中$\sigma\in\sum$就是每一个字母表中的元素，而最后三个则是正则表达式中定义的三种运算：

1. 闭包、迭代

   上文已介绍。

   $$A^*=\cup_{i\ge 0}A^i$$

2. 串接、连接

   注意这个操作是分前后的。

   $AB={ab|a\in A\ and\ b\in B}$

3. 并

   也就是集合中的并集

   $$A+B={s|s\in A\ or\ s\in B }$$

这三种运算的运算优先级由高到低排列，也就是说闭包的优先级最高，并的优先级最低。

注：

1. 语言学中的字是语意的基本单位，即语素；一个字可以拥有多个字形。
2. 有时也被记作$\lambda$。

参考资料：

1
2
3
4
5
6
7

[1] Wikipedia contributors. (2021, January 3). Regular language. In *Wikipedia, The Free Encyclopedia*. Retrieved 17:50, March 30, 2021, from https://en.wikipedia.org/w/index.php?title=Regular_language&oldid=998010276

[2] Wikipedia contributors. (2021, March 28). Formal language. In Wikipedia, The Free Encyclopedia. Retrieved 17:53, March 30, 2021, from https://en.wikipedia.org/w/index.php?title=Formal_language&oldid=1014601092

[3] Hopcroft, J. E., & Ullman, J. D. (1979). Introduction to Automata Theory, Languages and Computation (Addison-Wesley series in computer science) (1st ed.). Addison-Wesley Publishing Company.

[4] Formal language - Encyclopedia of Mathematics. (2019). Encyclopedia of Mathematics. https://encyclopediaofmath.org/index.php?title=Formal_language

CS143 Lecture04 Implementation of Lexical Analysis，Note

CS143 Lecture04 Implementation of Lexical Analysis

Implementation of regular expressions:

$$RegExp ⇒ NFA ⇒ DFA ⇒ Tables$$

Notation

• Union: $$A|B\equiv A+B$$
• Option: $$A+\epsilon\equiv A? $$
• Range: $$‘a’+‘b’+…‘z’\equiv [a-z]$$
• Excluded range: $$complement\ of\ [a-z]\equiv [\hat{} a ]$$

Regular Expressions => Lexical Spec. (1)

1. Write a regex for each token

2. Construct R, matching all lexemes for all tokens
   $$
   R = Keyword + Identifier + Number + …\
   = R1+ R2+ …
   $$
   (This step is done automatically by tools like Flex)

3. Let input be $$x_1…x_n$$ (iterate chars in input)

   For $$i \le i \le n$$ check
   $$
   x_1…x_i \in L®
   $$

4. If success, then we know that

   $$x_1…x_i \in L(R_j)$$ for some $$j$$

5. Remove $$x_1…x_i$$ from input and goto (3)

Ambiguities (1)

当
$$
x_1…x_i\in L®\
x_i…x_k\in L®
$$
上述两式同时成立时，换句话说，也就是多个起点相同，长度不同的子串同时满足语言$$L®$$时，

**Rule: ** Pick longest possible string in $$L®$$

也就是说取满足$$L®$$的最长子串。

Ambiguities (2)

当相同子串满足多个正则语言定义时，即
$$
x_1…X_i\in L(R_j)\
x_i…x_i\in L(R_k)
$$
这种给个优先级就好惹。

Error Handling

考虑如果一段输入的前缀无法被任何规则匹配的情况，我们会一直匹配直到输入终结处（EOF）。我们可以尝试编写一个匹配所有坏字符串的规则，并将其优先级设为最低。

Summary

Regular expressions provide a concise notation for string patterns.

Use in lexical analysis requires small extensions

• To resolve ambiguities
• To handle errors

Good algorithms known

• Require only single pass over the input
• Few operations per character (table lookup)

Finite Automata

A finite automaton consists of

• An input alphabet $$\sum$$
• A set of states $$S$$
• A start state $$n$$
• A set of accepting states $$F \subseteq S$$
• A set of transitions $$state \rightarrow^{input} state$$

Transitions

中文也就是状态转换。可以记作
$$
s_1 \rightarrow^{a} s_2
$$
可以读作输入$$a$$使状态$$s_1$$转移到状态$$s_2$$。

如果在输入结束时不处于接受状态(accept)，则拒绝(reject)该输入。

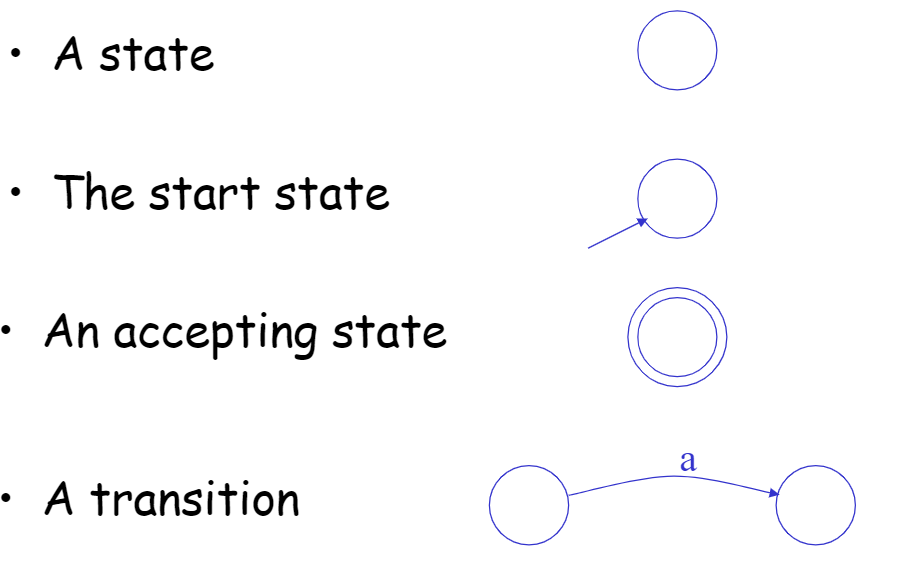
Epsilon Moves

This is a way to change a state to another without any input. 不过我真没找到这玩意的中文翻译，所以以下叫做ε-moves（大草

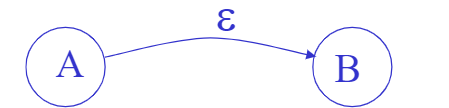
Only exist in NFAs.

Deterministic and Nondeterministic Automata

• Deterministic Finite Automaton

  每个输入都有确定的一个状态转移。

  没有ε-moves。

• Nondeterministic Finite Automata

  对于每个输入，状态转移的个数不确定。可以是零、一或多个状态转移。

  可以含有ε-moves。

所以，对于DFA来说，整个状态转移路径可以使用一个给定的输入确定。NFA则可以选择多种状态转移路径或是进行ε-moves。

因此我们规定：一个$$NFA$$如果可以达到一个最终状态，那么它是接受的（accept）。

$$NFA$$ vs. $$DFA$$

• $$DFA$$通常比$$NFA$$快
• $$DFA$$通常比$$NFA$$复杂（甚至可以达到指数级的）

对于$$NFA$$，它的状态数是可能状态数$$N$$的非空子集。也就是说，有$$2^N-1$$个可能状态数。

Convert Regular Expression to Finite Automata

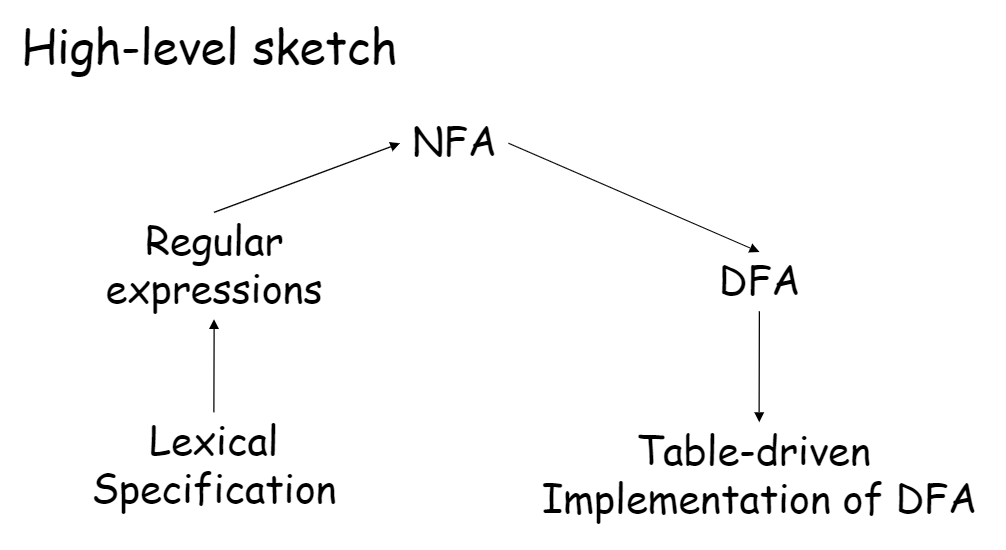
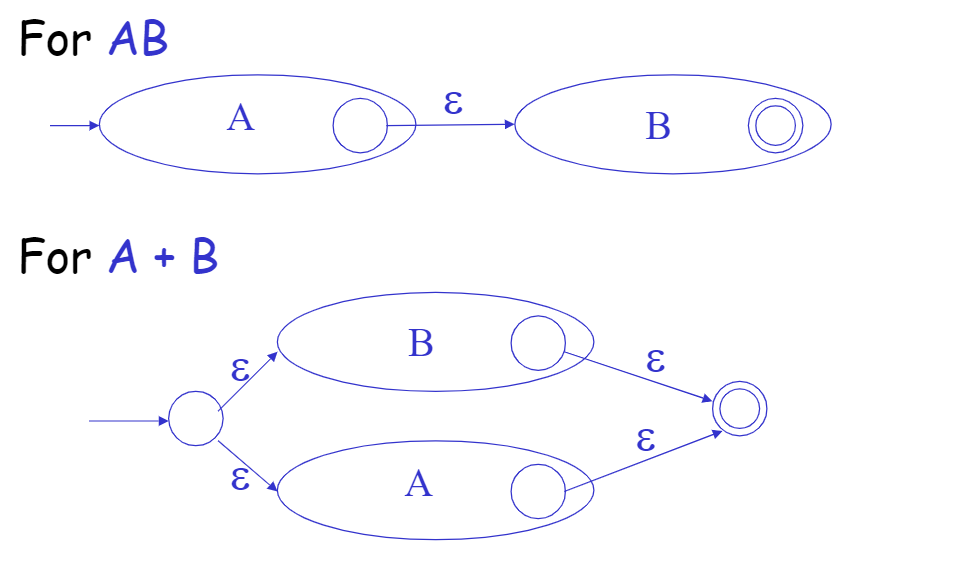
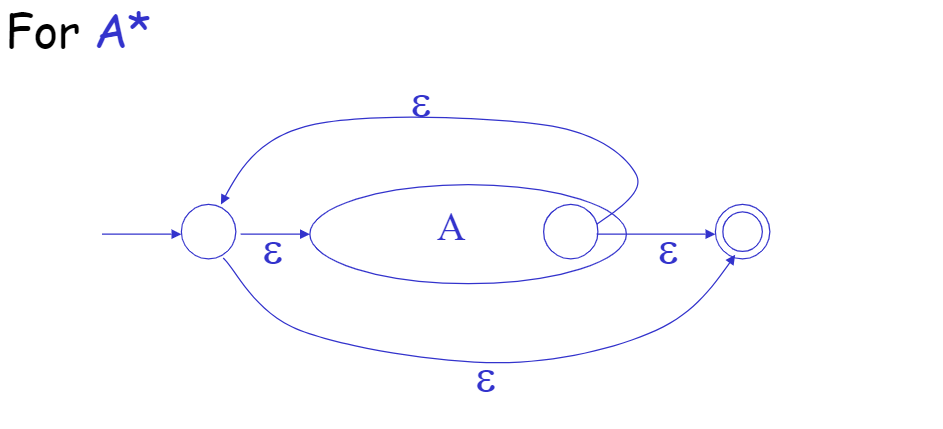
技巧

我们可以对$$NFA$$进行模拟。且目标$$DFA$$的每个状态都是一个$$NFA$$状态的非空子集。

目标$$DFA$$起始状态是一组从$$NFA$$的起始状态可以通过ε-moves转移到的状态。

而对于其它转换规则，我们遵从——如果状态$$S^$$在遇到输入$$a$$时，可以从原状态$$S$$达到（包括*ε-moves*），那么我们将$$S \rightarrow^{a} S^$$放进$$DFA$$的转换规则列表中。

实现

$$DFA$$可以通过一个二维数组$$T$$实现，我们将$$S_i\rightarrow^{a}S_k$$映射为$$T[i,a]=k$$。所以，$$T$$的一个维度代表状态，而另一个维度代表输入，其值代表目标状态。

执行$$DFA$$

如果当前状态为$$S_k$$，在读取输入$$a$$后，查表转移到状态$$S_i=T[k,a]$$。

结论

将$$NFA$$转换到$$DFA$$是很多像$$Flex$$这种工具的核心。但是因为$$DFA$$可能会有着极其巨大的状态数，所以，实践中通常会牺牲时间来换取空间。

CS143 Lecture03 Lexical Analysis，Note

CS143 Lecture03: Lexical Analysis

词法分析。

Goal: Partition input string into substring called tokens

Lexical analysis produces a stream of tokens, which is input to the parser.

这是编译的第1/4步，词法分析产生词元序列并作为下一阶段(parse，翻译)的输入。

Token

词元。

A syntactic category，也就是对句法的分类

In English:

• noun, verb, adjective, …

In a programming language:

• Identifier, Integer, Keyword, Whitespace, …

A token class corresponds to a set of strings.

Examples

• Identifier: strings of letters or digits, starting with a letter
• Integer: a non-empty string of digits
• Keyword: “else” or “if” or “begin” or …
• Whitespace: a non-empty sequence of blanks, newlines, and tabs

Design

噢对，这有个缩写N.B.，原版是Nota Bene（拉丁语），也就是划重点的意思。另外lexeme中文翻译为词素。

• Define a finite set of tokens.
• Describe which strings belong to each token.

但是我们应该考虑到歧义。如下例子：

i/if；=/==；Foo<Bar>/cin >> var;/Foo<Bar<Bazz>>；

而要消除歧义显然就没办法在线处理了——我们需要“Lookahead”。

现在我们需要的，是描述词元的词素并找到一种消除歧义的方法。

Regular Languages

中文叫做正则语言或是正规语言。正则语言是描述词元的最常用的形式。

Language Def. : Let S be a set of characters. A language over S is a set of strings of characters drawn from S.

定义指出，字符串S上的语言就是一组S上的子串。$$L(x)$$表示“x的语言”。

所以，

• 语言是一组字符串。
• 需要一些记号来指定词法分析器所需的字符串组。
• 正则语言使用的标准记号叫做正则表达式。

Atomic Regular Expression

• Single character

  $$‘c’={“c”}$$

• Epsilon

  $$\epsilon = {“”}$$

Compound Regular Expression

• Union 并

  $$A+B={s|s \in A \ \ or\ \ s\in B}$$

  也就是对$$A$$和$$B$$所表示的语言取并集。

• Concatenation 串接

  $$AB={ab|a\in A\ \ and\ \ b \in B}$$

• Iteration 克林闭包

  $$A^*=\cup_{i\ge 0}A^i$$ where $$A^i=A…i \ \ times\ \ …A$$

  表示$$A$$中的字符串没有出现或是多次出现。

  注意以上运算的优先级是$$闭包(最高)-串接-并(最低)$$。

Regular Expression Def. : The regular expressions over S are the smallest set of expressions including

• $$\epsilon$$
• $$‘c’$$ where $$c\in \sum$$
• $$A+B$$ where $$A,B$$ are regex over $$\sum$$
• $$AB$$
• $$A^*$$ where $$A$$ is regex over $$\sum$$

Syntax vs. Semantics

To be careful, we should distinguish syntax and semantics.

$$L(\epsilon) = {“”}$$

$$L(‘c’)={“c”}$$

$$L(A+B)=L(A)\cup L(B)$$

$$L(AB)={ab|a\in L(A)\ \ and\ \ b \in L(B)}$$

$$L(A^*)=\cup_{i\ge 0}L(A^i)$$

Example

Keyword

Keyword: “else” or “if” or “begin” or …

$$‘else’+‘if’+‘begin’+…$$

Note: $$‘else’$$ abbreviates $$‘e’\ ‘l’\ ‘s’\ ‘e’$$

Integer

In order to describe integers, here is an abbreviation:

$$A^+=AA^$$
$$
⇒ digit=‘0’+‘1’+‘2’+‘3’+‘4’+‘5’+‘6’+‘7’+‘8’+‘9’\
⇒ integer=digit^+
$$
Identifier
$$
letter=‘A’+…+‘Z’+‘a’+…+‘z’\
identifier=letter(letter+digit)^
$$
Whitespace
$$
(‘\ ‘+’\backslash n’ + ‘\backslash t’)
$$

Summary

• Regular languages are a language specification
  • We still need an implementation
• Given a string s and a rexp R, is
  • $$s \in L®$$ ?

CS143 Lecture01 Overview，Note

CS143 Leture01: Overview，Note

The structure of a compiler

1. Lexical Analysis(词法分析)
2. Parsing(预处理)
3. Semantic Analysis(文法分析)
4. Optimization(优化)
5. Code Generation(代码生成)

Lexical Analysis

• Recognize words.

  word is the smallest unit above letters.

• Lexical Analysis divide a string into “words” or “token”

Parsing

Parsing = Diagramming Sentences

Semantic Analysis

To understand the meaning of sentence, but meaning is too hard to a program.

Compilers perform limited semantic analysis to catch inconsistencies.

Optimization

CS243: Program Analysis and Optimization

Code Generation

A translation to another language, and typically produce assembly code.

Intermediate Representations（中间形式，a.k.a. IR）

Many compilers will perform translations between successive intermediate languages（很多编译器翻译时会使用多个中间形式.）

• All but first and last are intermediate representations (IR) internal（内部的） to the compiler.

IRs are useful to hide the lower levels feature from higher levels.

• registers
• memory layout
• raw pointers
• …

CS143 Lecture02 Language Design and Instruction of Cool，Note

CS 143 Lecture02: Language Design and Instruction of Cool

Topics:

• Why are there new languages?
• Good-language criteria

History of ideas:

• Abstract(抽象)
• Types(类型)
• Reuse(复用)

History of Ideas

• Abstract

  Abstraction = Ignorance of some details

  Abstract is necessary to build a complex system, and the key is information hiding - only expose the essential

  Modes:

  • Via language
  • Via function / subroutine (LISP?)
  • Via module (ECMAScript)
  • Via class or abstract data types (Rust)

• Types

  • Originally, few(no) types
  • But types helps on building abstractions / compile time check.
  • Experiments with various forms of parameterization(a.k.a. generic types，也就是所谓“泛型”).
  • Best developed in functional programming(a.k.a. FP).

• Reuse

  It’s many common patterns while programming, but they’re hard to reuse.

  Tow popular approaches:

  • Type parameterization（泛型，List<int>、List<double>）
  • Classes and inheritance
  • （Where is Traits? 🤣

Darc Bot更新记录

Changelogs

…

2021/2/15

• 命运2信息查询
• 数据库问题临时修复

2021/2/14

• 彩六战绩查询
• 切换到TypeScript

Halo, 哈喽

欢迎来到Darc的小博客啦~

尘尘杂记 | 风

唔。

总是想，人，是不是就是在旦夕之间游走的蜉蝣啊。“朝而往，暮而归”，以此为乐。